感觉最难想的就是前期的博弈了。后面 ddp 就很套路。
解法
这种问题首先要先忽略修改操作。如果没有修改操作,那我们设状态 $f_i$ 表示在第 $i$ 格是否先手必胜。如果后面 $m$ 格存在先手必败状态,则在第 $i$ 格一定是先手必胜的。
如果后面 $m$ 格都是先手必胜的,那显然双方都不想主动走到后面 $m$ 格中,双方会轮流在当前格子中消耗,知道当前格子的数为 $0$。所以状态只与 $a_i$ 的奇偶性有关。
其实这是一种从 $[f_{i+1}\ f_{i+2}\ \dots\ f_{i+m}]$ 到 $[f_i\ f_{i+1}\ \dots\ f_{i+m-1}]$ 的变换,我们可以将这个行向量状压,值域不超过 $2^5$。变换的更形式如图所示。
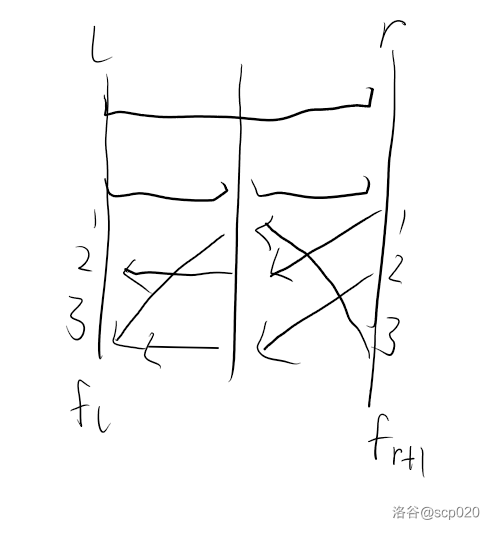
通过图我们不难发现这种变换是有结合律的,所以可以使用线段树维护区间变换的结果,设线段树节点表示区间为 $[l,r]$,区间的变换即为 $f_{r+1}$ 进行了这一区间中一些列的变换 $f_l$ 的值会是多少。然后我们就很自然的支持了单点修改 $a_i$ 的操作。
现在考虑如何支持区间修改。
注意到转移只与 $a_i$ 的奇偶性有关,而且区间加一个数会同步改变这个区间所有数的奇偶性,而且变换只有两种,而且还有括号修复那题的 trick,我们考虑把每个节点的两种变换都存下来,如果区间修改不改变奇偶性的话我们就忽略操作,否则即为交换两种变换。
然后就做完了。
代码
#include<bits/stdc++.h>
namespace fast_IO
{
/**
* useless things
*/
};
using namespace fast_IO;
int n,m,q,a[200010];
struct transform
{
int a[32];
inline transform()
{
memset(a,0,sizeof(a));
}
inline int &operator[](const int ind) noexcept
{
return a[ind];
}
};
struct node
{
transform *now,*opp;
int lazy;
node *lc,*rc;
node()
{
now=new transform(),opp=new transform(),lazy=0,lc=rc=nullptr;
}
inline void pushup()
{
for(int i=0;i<=(1<<m)-1;i++)
now->a[i]=lc->now->a[rc->now->a[i]],
opp->a[i]=lc->opp->a[rc->opp->a[i]];
}
inline void pushdown()
{
if(lazy)
{
std::swap(lc->now,lc->opp),std::swap(rc->now,rc->opp),lc->lazy^=1,rc->lazy^=1,lazy=0;
}
}
};
class seg_tree
{
#define ls l,mid
#define rs mid+1,r
private:
node *root;
inline node *build(int l,int r)
{
node *rt=new node();
if(l==r)
{
for(int i=0;i<(1<<m)-1;i++) rt->now->a[i]=rt->opp->a[i]=(i*2+1)%(1<<m);
rt->now->a[(1<<m)-1]=((1<<m)-1)^a[l],rt->opp->a[(1<<m)-1]=rt->now->a[(1<<m)-1]^1;
}else
{
int mid=(l+r)/2;
rt->lc=build(ls),rt->rc=build(rs),rt->pushup();
}
return rt;
}
inline void fix(node *rt,const int L,const int R,int l,int r)
{
if(L<=l && r<=R)
{
std::swap(rt->now,rt->opp),rt->lazy^=1;
return;
}
int mid=(l+r)/2;
rt->pushdown();
if(L<=mid) fix(rt->lc,L,R,ls);
if(R>mid) fix(rt->rc,L,R,rs);
rt->pushup();
}
inline transform ask(node *rt,const int L,const int R,int l,int r)
{
if(L<=l && r<=R) return *(rt->now);
int mid=(l+r)/2;
rt->pushdown();
if(L>mid) return ask(rt->rc,L,R,rs);
if(R<=mid) return ask(rt->lc,L,R,ls);
transform ll=ask(rt->lc,L,R,ls),rr=ask(rt->rc,L,R,rs),ret;
for(int i=0;i<=(1<<m)-1;i++) ret[i]=ll[rr[i]];
return ret;
}
public:
inline void build()
{
root=build(1,n);
}
inline void fix(const int L,const int R,const long long val)
{
if(val&1) fix(root,L,R,1,n);
}
inline int ask(const int L,const int R)
{
return 2-(ask(root,L,R,1,n)[(1<<m)-1]&1);
}
};
seg_tree tree;
long long tmp;
signed main()
{
in>>n>>m>>q;
for(int i=1;i<=n;i++) in>>tmp,a[i]=tmp&1;
tree.build();
for(int i=1,op,x,y;i<=q;i++)
{
in>>op>>x>>y;
if(op==1) in>>tmp,tree.fix(x,y,tmp);
else out<<tree.ask(x,y)<<'\n';
}
fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
return 0;
}