非常好构造题,使我的草稿纸旋转。
解法
我们记输入的数组为 $a$,需要输出的两个数组为 $b,c$(因为当时起变量名起的)。
考虑利用 $a_i$ 互不相同的性质。
先将 $a_i$ 升序排序。因为题中保证 $a_i$ 互不相同,所以相邻两数的差至少为 $1$,从而 $a_i \ge i - 1$。
考虑到最多有 $\lceil \dfrac{n}{3} \rceil$ 个重复数字,即为需要至少有 $\lfloor \dfrac{2n}{3} \rfloor$ 种不同数字。我们可以将整个数组等分为 $3$ 段,分别是 $[1,\lfloor \dfrac{n}{3} \rfloor ]$,$(\lfloor \dfrac{n}{3} \rfloor,\lfloor \dfrac{2n}{3} \rfloor]$,$(\lfloor \dfrac{2n}{3} \rfloor,n]$。具体构造如下图。
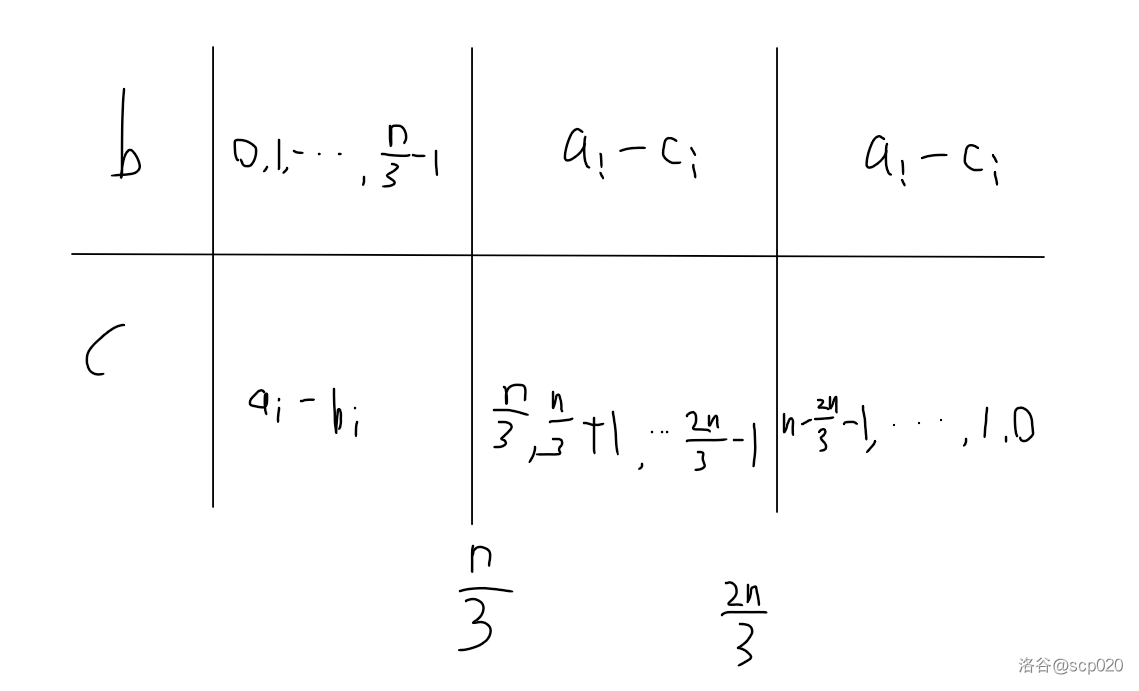
为什么这么构造是对的?
显然对于 $c$ 数组,第二段和第三段的数互不相同,满足至少有 $\lfloor \dfrac{2n}{3} \rfloor$ 种不同数字。考虑为什么 $b$ 数组至少有 $\lfloor \dfrac{2n}{3} \rfloor$ 种不同数字。
观察第一段和第三段,因为 $a_i \ge i-1$,所以第三段的第一个 $a_i$ 满足 $a_i \ge \dfrac{2n}{3}$,而 $n - \lfloor \dfrac{2n}{3} \rfloor -1 = \lceil \dfrac{n}{3} \rceil - 1$,所以 $c_i$ 满足 $c_i \ge \dfrac{n}{3}$,而在第三段 $a$ 单调上升,$c$ 单调下降,所以 $b$ 单调上升,所以 $b$ 数组在第一段和第三段互不相同。
代码
#include<bits/stdc++.h>
namespace fast_IO
{
/**
* 没啥用的快读快写
*/
};
using namespace fast_IO;
int n,b[100010],c[100010],fir,sec;
struct node
{
int val,ord;
inline bool operator<(const node rhs) const
{
return val<rhs.val;
}
};
node a[100010];
int main()
{
in>>n,fir=n/3,sec=n*2/3;
for(int i=1;i<=n;i++) in>>a[i].val,a[i].ord=i;
std::sort(a+1,a+n+1);
for(int i=1;i<=fir;i++) b[a[i].ord]=i-1,c[a[i].ord]=a[i].val-b[a[i].ord];
for(int i=fir+1;i<=sec;i++) c[a[i].ord]=i-1,b[a[i].ord]=a[i].val-c[a[i].ord];
for(int i=n;i>sec;i--) c[a[i].ord]=n-i,b[a[i].ord]=a[i].val-c[a[i].ord];
out<<"YES\n";
for(int i=1;i<=n;i++) out<<b[i]<<' ';
out<<'\n';
for(int i=1;i<=n;i++) out<<c[i]<<' ';
fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
return 0;
}