水紫,建议降蓝。
解法
求线段相交裸题,考虑使用向量解决。
我们把矩形的 $4$ 个点两两相连,得到 $6$ 条线段,如果先输入的线段和这 $6$ 条线段都没有交点,则认为线段和矩形不相交,否则认为相交。
向量求两线段是否相交分为两步,快速排斥实验和跨立实验。为了表述方便,我们记两线段分别为 $AB,CD$。
快速排斥实验
分别以 $AB$ 和 $CD$ 为对角线做水平竖直的两个矩形。如果两个矩形没有相交部分,那两线段不可能相交,我们称为未通过快速排斥实验。否则我们称为通过快速排斥实验。如图。
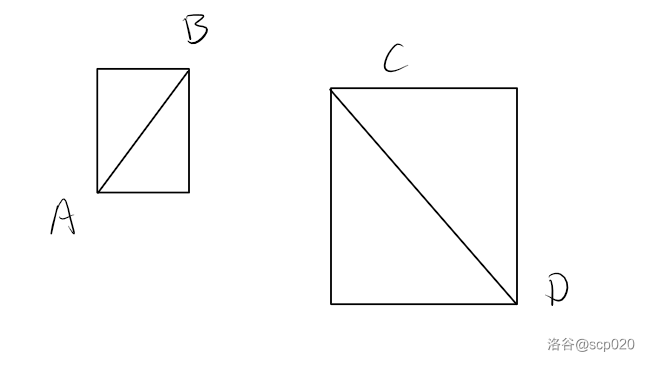
跨立实验
当两线段通过快速排斥实验后,则进行跨立实验。跨立实验即为:验证点 $C,D$ 是否在直线 $AB$ 的两侧同时点 $A,B$ 是否在直线 $CD$ 的两侧。
根据向量叉乘的几何意义,$\overrightarrow{AB} \times \overrightarrow{AC}$ 为正代表点 $C$ 在直线 $AB$ 的逆时针方向,为 $0$ 代表点 $C$ 在直线 $AB$ 上,为负代表点 $C$ 在直线 $AB$ 的顺时针方向。
如果 $\overrightarrow{AB} \times \overrightarrow{AC}$ 和 $\overrightarrow{AB} \times \overrightarrow{AD}$ 正负性不同,$\overrightarrow{CD} \times \overrightarrow{CA}$ 和 $\overrightarrow{CD} \times \overrightarrow{CB}$ 正负性不同,我们称为通过跨立实验。
如果两线段通过了快速排斥实验和跨立实验,则我们认为两线段相交。
为什么要有快速排斥实验
好多人读到了这里,感觉跨立实验足以应付线段相交,为什么还要有快速排斥实验呢?
其实这并不是在减少计算过程,而是保证正确性。如图。
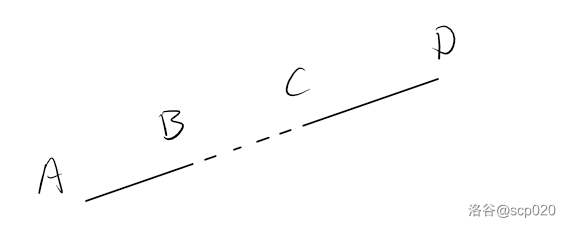
两线段会通过跨立实验,如果不进行快速排斥实验,那我们就会错误的认为两线段相交。
代码
#include<bits/stdc++.h>
namespace fast_IO
{
/**
* 快读快写
*/
};
using namespace fast_IO;
#define int long long
int t,X1,Y1,X2,Y2;
struct point
{
int x,y;
point()
{
x=y=0;
}
point(int x,int y)
{
this->x=x,this->y=y;
}
inline point operator-(const point &rhs) const
{
return point(x-rhs.x,y-rhs.y);
}
inline int operator*(const point &rhs)
{
return x*rhs.y-y*rhs.x;
}
};
point po1,po2,po3,po4;
inline int sgn(int x)
{
return x==0?0:(x>0?1:-1);
}
struct seg
{
point s,t;
inline friend bool cross(const seg &lhs,const seg &rhs)
{
return std::max(lhs.s.x,lhs.t.x)>=std::min(rhs.s.x,rhs.t.x) &&
std::max(lhs.s.y,lhs.t.y)>=std::min(rhs.s.y,rhs.t.y) &&
std::max(rhs.s.x,rhs.t.x)>=std::min(lhs.s.x,lhs.t.x) &&
std::max(rhs.s.y,rhs.t.y)>=std::min(lhs.s.y,lhs.t.y) &&
sgn((rhs.s-lhs.s)*(lhs.t-lhs.s))*sgn((rhs.t-lhs.s)*(lhs.t-lhs.s))<=0 &&
sgn((lhs.s-rhs.s)*(rhs.t-rhs.s))*sgn((lhs.t-rhs.s)*(rhs.t-rhs.s))<=0;
}
};
seg a,s1,s2,s3,s4,s5,s6;
signed main()
{
in>>t;
while(t--)
{
in>>a.s.x>>a.s.y>>a.t.x>>a.t.y>>X1>>Y1>>X2>>Y2;
if(X1>X2) std::swap(X1,X2);
if(Y1>Y2) std::swap(Y1,Y2);
po1=(point){X1,Y1},po2=(point){X1,Y2},po3=(point){X2,Y1},po4=(point){X2,Y2};
s1=(seg){po1,po2},s2=(seg){po2,po4},s3=(seg){po4,po3},s4=(seg){po3,po1};
s5=(seg){po1,po4},s6=(seg){po2,po3};
if(!cross(a,s1) && !cross(a,s2) && !cross(a,s3) && !cross(a,s4) && !cross(a,s5) && !cross(a,s6))
out<<"F\n";
else out<<"T\n";
}
fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
return 0;
}