感谢战学长的帮助。
解法
本题的关键是将多边形 $Q$ 分割为两部分,一部分是由点 $a,b,c$ 组成的三角形,另一部分是由从 $b$ 到 $c$ 这 $k + 1$ 个点组成的凸多边形。注意到这种由 $k + 1$ 个点组成的凸多边形的数量是有限的,为 $n$ 个,而由点 $a,b,c$ 组成的三角形的数量更多,所以我们考虑固定 $k + 1$ 个点的多边形,即固定点 $b,c$,然后查找可以使三角形 $a,b,c$ 面积最大的点 $a$,即点 $a$ 到直线 $bc$ 的垂直距离最大。
考虑所有可被选择为点 $a$ 的点,它们和直线 $bc$ 的距离是一个单峰函数,故可以考虑使用三分法求得函数峰值。
现在我们想到了一个做法:用 $\mathcal{O}(n + k)$ 的时间复杂度预处理所有 $k + 1$ 个点的多边形的面积,用 $\mathcal{O}(n \log n)$ 的时间复杂度求得点 $a$。
预处理多边形面积的方法:先选定一个多边形,将其暴力地拆成 $k-1$ 个三角形,对每个三角形叉积求面积,值得注意的是叉积的模长是平四的有向面积,所以这里求面积时应对叉积的模长取绝对值。这里有个小 $trick$,就是在计算过程中我们不将面积除以 $2$,而是在最后输出时除以 $2$,防止计算过程中有浮点数的出现。
然后考虑递推转移,如图,目标状态的面积为原有状态的面积加上红色三角形面积减去绿色三角形面积。
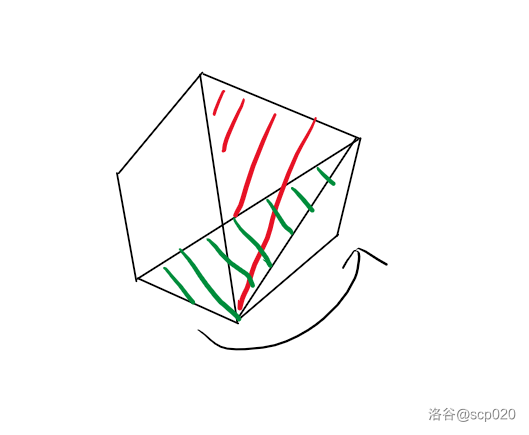
这时战学长给我发了个 $hint$,说有严格线性做法。仔细考虑当线段 $bc$ 逆时针变化时,$a$ 点也是逆时针变化的。所以 $a$ 点的移动是有单调性的,移动次数不超过 $n$ 次,因此可以每次旋转线段 $bc$ 时暴力地移动点 $a$。
时间复杂度 $\mathcal{O}(n + k)$。
代码
#include<bits/stdc++.h>
namespace fast_IO
{
/**
* 顾名思义,是快读快写。
*/
};
using namespace fast_IO;
#define int long long
// considering the issue of accuracy,we can twice the storage surface
int t,n,k,surf[100010],pt,b,c,pres,nxts,ans;
struct point
{
int x,y;
inline point(int x=0,int y=0)
{
this->x=x,this->y=y;
}
inline point operator-(const point &rhs) const
{
return point(x-rhs.x,y-rhs.y);
}
inline int operator*(const point &rhs)
{
return x*rhs.y-y*rhs.x;
}
};
point a[100010];
inline int calc(const point x,const point y,const point z) // calculate the surface of the triangle we chose
{
return abs((y-x)*(z-x));
}
signed main()
{
in>>t;
while(t--)
{
in>>n>>k,ans=0;
for(int i=1;i<=n;i++) in>>a[i].x>>a[i].y,surf[i]=0;
b=1,c=k+1,pt=c,pres=0;
for(int i=2;i<=k;i++) surf[b]+=calc(a[i-1],a[i],a[c]);
for(int i=2;i<=n;i++)
surf[i]=
surf[i-1]+
calc(a[i+k-1>n?i+k-1-n:i+k-1],a[i+k>n?i+k-n:i+k],a[i])-
calc(a[i-1],a[i+k-1>n?i+k-1-n:i+k-1],a[i]);
for(;b<=n;b++,c=b+k>n?b+k-n:b+k)
{
pres=calc(a[b],a[c],a[pt]);
while(pt!=b)
{
nxts=calc(a[b],a[c],a[pt+1>n?pt+1-n:pt+1]);
if(nxts>pres) pres=nxts,pt=pt+1>n?pt+1-n:pt+1;
else break;
}
ans=std::max(ans,surf[b]+pres);
if(pt==c) pt=pt+1>n?pt+1-n:pt+1;
}
out<<ans/2.0<<'\n';
}
fwrite(Ouf,1,p3-Ouf,stdout),fflush(stdout);
return 0;
}