集训考到的题,赛时没想出来,很巧妙的做法。
解法
前置芝士:线段树,二分。
注意到题面要我们求最早与前面的条件有矛盾的条件的编号,所以这个答案是有单调性的,即假设前 $i$ 个条件有矛盾,则对于所有的 $j > i$,前 $j$ 个条件也有矛盾。相应的,对于所有的 $j < i$,前 $j$ 个条件没有矛盾。就此单调性,我们考虑二分答案。下面考虑如何写这个 check。
考虑什么时候条件之间有矛盾,分两种情况,如下图所示。
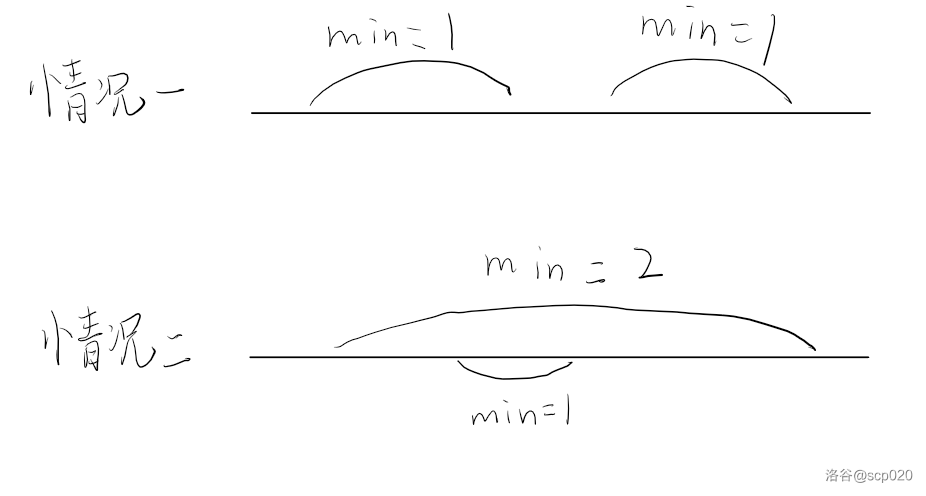
-
因为题中说数组中的数字互不相同,所以如果两个相离的区间的最小值相同,则两条件一定矛盾。这个情况显然。
-
如果区间 $A$ 包含区间 $B$,且区间 $A$ 的最小值大于区间 $B$ 的最小值则两条件一定矛盾。这个情况显然。
所以我们使用线段树标记区间,看是否违反情况二。用简单的循环就可以判断是否违反情况一。
代码
#include<bits/stdc++.h>
using namespace std;
namespace fast_IO
{
/*
fast input/output
*/
};
using namespace fast_IO;
int n,q,l=1,r,mid,ans;
/**
* seg_node:
* 1. sum,lazy,lc,rc
* 2. pushup
* 3. pushdown
*
* segment_tree:
* 1. build
* 2. clear
* 3. fix
* 4. ask
*/
#define ls l,mid
#define rs mid+1,r
struct seg_node
{
int sum,lazy;
seg_node *lc,*rc;
inline void pushup()
{
sum=lc->sum+rc->sum;
}
inline void pushdown(const int &l,const int &r)
{
if(lazy)
{
int mid=(l+r)/2;
lc->sum=mid-l+1,rc->sum=r-mid,lc->lazy=rc->lazy=1,lazy=0;
}
}
};
class seg_tree
{
private:
seg_node *root;
inline seg_node *build(int l,int r)
{
seg_node *rt=new seg_node;
if(l<r)
{
int mid=(l+r)/2;
rt->lc=build(ls),rt->rc=build(rs);
}
return rt;
}
inline void clear(seg_node *rt,int l,int r)
{
rt->sum=rt->lazy=0;
if(l<r)
{
int mid=(l+r)/2;
clear(rt->lc,ls),clear(rt->rc,rs);
}
}
inline void fix(seg_node *rt,const int &L,const int &R,int l,int r)
{
if(L<=l && r<=R)
{
rt->sum=r-l+1,rt->lazy=1;
return;
}
rt->pushdown(l,r);
int mid=(l+r)/2;
if(L<=mid) fix(rt->lc,L,R,ls);
if(R>mid) fix(rt->rc,L,R,rs);
rt->pushup();
}
inline int ask(seg_node *rt,const int &L,const int &R,int l,int r)
{
if(L<=l && r<=R) return rt->sum;
rt->pushdown(l,r);
int mid=(l+r)/2,ret=0;
if(L<=mid) ret+=ask(rt->lc,L,R,ls);
if(R>mid) ret+=ask(rt->rc,L,R,rs);
return ret;
}
public:
inline void build()
{
root=build(1,n);
}
inline void clear()
{
clear(root,1,n);
}
inline void fix(const int &L,const int &R)
{
fix(root,L,R,1,n);
}
inline int ask(const int &L,const int &R)
{
return ask(root,L,R,1,n);
}
};
seg_tree tree;
struct que
{
int l,r,x;
inline bool operator<(const que &rhs) const
{
return x>rhs.x;
}
};
que a[25010],tmp[25010];
inline bool judge(int x)
{
for(int i=1;i<=x;i++) tmp[i]=a[i];
sort(tmp+1,tmp+x+1),tree.clear();
for(int i=1,j,l1,l2,r1,r2;i<=x;i=j)
{
j=i,l1=l2=tmp[i].l,r1=r2=tmp[i].r;
while(tmp[i].x==tmp[j].x && j<=x) j++;
for(int k=i;k<j;k++)
l1=min(l1,tmp[k].l),r1=max(r1,tmp[k].r),l2=max(l2,tmp[k].l),r2=min(r2,tmp[k].r);
if(l2>r2) return false;
if(tree.ask(l2,r2)==r2-l2+1) return false;
tree.fix(l1,r1);
}
return true;
}
int main()
{
read(n),read(q),r=q,tree.build();
for(int i=1;i<=q;i++) read(a[i].l),read(a[i].r),read(a[i].x);
while(l<=r)
{
mid=(l+r)/2;
if(judge(mid)) l=mid+1;
else ans=mid,r=mid-1;
}
cout<<ans;
return 0;
}